Introduction #
Un document scientifique ou qui traite d’informatique contient des explications, des démonstrations, du code informatique, des données. Il est très pratique de travailler sur un document qui lie tous ces éléments ensembles… Une des difficultés vient du code, l’idéal c’est de pouvoir l’exécuter et que les résultats viennent mettre à jour le document automatiquement. org-mode apporte une réponse à cette problématique via l’extension babel. Cette extension permet de réaliser des calepins dynamiques et exportable en pdf.
Voici un exemple de calepin réalisé avec org-mode.1
Méthode de Héron #
La méthode de Héron permet de calculer une racine carrée.
Approche géométrique #
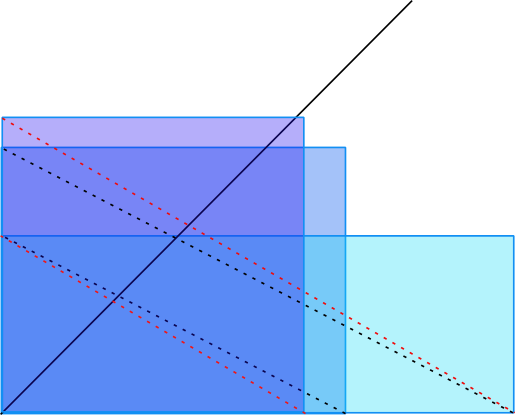
Il est intéressant de mettre en évidence le principe géométrique sous-jacent à la méthode. Chez les mathématiciens grecs, extraire la racine carrée de \(a\) revient à trouver un carré dont l’aire soit \(a\). En prenant un rectangle de côté arbitraire \(x\) et de même aire, il est nécessaire que l’autre côté ait pour longueur \(\frac a x\). Pour le rendre « moins rectangle », il suffit de considérer un nouveau rectangle dont la longueur est la moyenne arithmétique des deux côtés précédents soit \(\dfrac {x+\frac a x}2\) et dont l’aire reste \(a\).
En réitérant infiniment le processus, le rectangle se transforme petit à petit en un carré de même aire. Cette constatation est à la base de la méthode de Héron
Principe #
Pour déterminer la racine carrée du nombre (positif) \(a\), il convient de considérer la suite définie par récurrence de la façon suivante : \[\forall n\in \mathbb {N} \quad x_{n+1}= \frac {x_n + \frac {a}{x_n}}2\]
de premier terme \(x_0>0\) choisi si possible « assez proche » de \(\sqrt a\).
La suite ainsi obtenue est une suite décroissante à partir du second terme, convergeant vers \(\sqrt a\).
Application à \(\sqrt 2\) #
def heron(a:float=2,x0:int=1,n:int=5):
s:float =x0
for i in range(n):
s=(s+a/s)/2
return s
heron()
1.414213562373095
Écart avec \(\sqrt{2}\)
from math import sqrt
sqrt(2)
abs(sqrt(2)-heron())
2.220446049250313e-16
Astuce: Pour obtenir la console IPython , place-toi dans le bloc de code puis
C-c C-v C-z.
C’est très pratique tu peux expérimenter dans la console et écrire ton document en parallèle.
Application aux grands nombres #
La fonction \(\sqrt{}\) ne permet pas de calculer la racine carrée pour les grands nombres.
sqrt(10**2025)
Renvoie une erreur…
OverflowError Traceback (most recent call last) Cell In[259], line 1 —-> 1 sqrt(10**2025)
OverflowError: int too large to convert to float
Essayons une autre approche…
\(\sqrt{10^{2025}}=\sqrt{10}\sqrt{10^{2024}}=\sqrt{10}\cdot10^{1012}\simeq 3\cdot 10^{1012}\).
Ainsi \(3\cdot 10^{1012}\) est un entier proche de \(\sqrt{10^{2025}}\).
On cherche deux entiers consécutifs qui encadre \(\sqrt{10^{2025}}\).
On va travailler uniquement avec des entiers… d’où la division entière en python : // .
def heronGN(a:int=2,x0:int=1):
s:int =0
t:int=x0
while t!=s:
s=t
t=int((s+a//s)//2)
return s
ra=heronGN(10**2025,3*10**1012)
Écart relatif entre \(ra^2\) et \(a\).
(ra**2-10**2025)/10**2025
-0.0
Écart relatif entre \((ra+1)^2\) et \(a\).
((ra+1)**2-10**2025)/10**2025
0.0
Donc \(\sqrt{10^{2025}}\) vaut à une unité près par défaut:
ra
31622776601683793319988935444327185337195551393252168268575048527925944386392382213442481083793002951873472841528400551485488560304538800146905195967001539033449216571792599406591501534741133394841240853169295770904715764610443692578790620378086099418283717115484063285529991185968245642033269616046913143361289497918902665295436126761787813500613881862785804636831349524780311437693346719738195131856784032312417954022183080458728446146002535775797028286440290244079778960345439891633492226526120677926516760310484366977937569261557205003698949094694218500073583488446438827311092891090423480542356534039072740197865437259396417260013069900009557844631096267906944183361301813028945417033158077316263863951937937046547652206320636865871978220493124260534541116093569798281324522970007988835237595853285792513629646865114976752171234595592380393756251253698551949553250999470388439903364661654706472349997961323434030218570521878366763457895107329828751579452157716521396263244383990184845609357626020316768042407
Python, matplotlib et seaborn #
Matplotlib #
Matplotlib est une bibliothèque très populaire pour réaliser des graphiques.
import numpy as np
from numpy import linalg as la
import matplotlib
import matplotlib.cm as cm
import matplotlib.pyplot as plt
xmin=-1
xmax=2.3
ymin=-1
ymax=2.5
delta=0.1
def g(x,y):
return (x**(2)+y-2)*(y**(2)-x-1)**(2)+x**(2)-2*y+2
X=np.arange(xmin,xmax,delta)
Y=np.arange(ymin,ymax,delta)
U, V = np.meshgrid(X, Y)
Z=g(U,V)
fig = plt.figure(figsize=plt.figaspect(1))
ax = fig.add_subplot(1, 1, 1, projection='3d')
# plot a 3D surface like in the example mplot3d/surface3d_demo
surf = ax.plot_surface(U, V, Z, rstride=1, cstride=1, cmap=cm.coolwarm,
linewidth=0, antialiased=False)
#ax.set_zlim(-1.01, 1.01)
fig.colorbar(surf, shrink=0.5, aspect=10)
plt.savefig('images/plot3d.png')
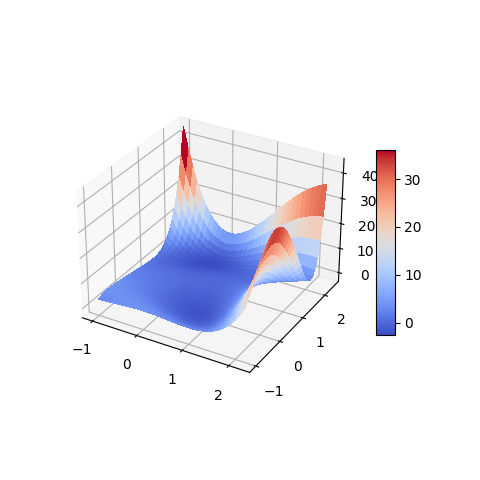
Seaborn #
Seaborn est une autre bibliothèque, qui repose sur matplotlib, elle propose une syntaxe de plus haut niveau qui simplifie la création de graphique; notamment dans le domaine statistique.
import matplotlib.pyplot as plt
import seaborn as sns
plt.figure(figsize=(5, 5))
tips = sns.load_dataset("tips")
sns.boxplot(x="day", y="tip", data=tips)
plt.savefig('images/boxplot2.png')
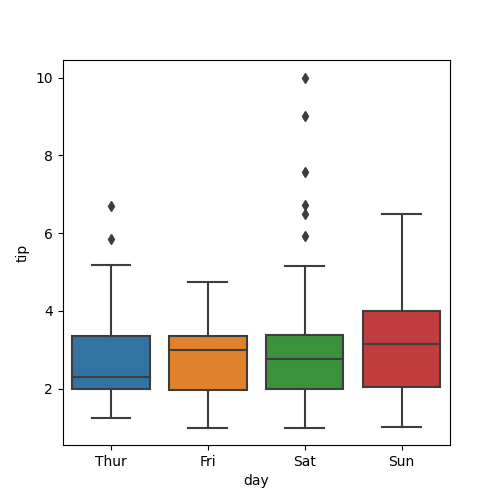
D’autres exemples d’utilisation de org-babel #
D’autres types de bloc exécutables sont disponibles
Xcas #
developper((x+2)^7)
\(x^{7}+14 x^{6}+84 x^{5}+280 x^{4}+560 x^{3}+672 x^{2}+448 x+128\)
Plantuml #
Graphe #
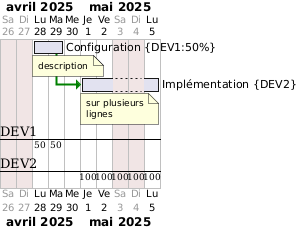
Diagramme de Gantt #
https://plantuml.com/gantt-diagram
Et bien d’autres… #
https://orgmode.org/worg/org-contrib/babel/languages/index.html
| Language | Identifier | Documentation | Maintainer |
|---|---|---|---|
| C | C | ob-doc-c | Thierry Banel |
| C++ | cpp | ob-doc-c | Thierry Banel |
| Calc | calc | Tom Gillespie | |
| Clojure | clojure | ob-doc-clojure | Daniel Kraus |
| CSS | css | ob-doc-css | |
| ditaa | ditaa | ob-doc-ditaa | |
| Gnuplot | gnuplot | ob-doc-gnuplot | Ihor Radchenko |
| Graphviz | dot | ob-doc-dot | Justin Abrahms |
| Java | java | ob-doc-java | Ian Martins |
| Julia | julia | ob-doc-julia | Pedro Bruel |
| LaTeX | latex | ob-doc-LaTeX | |
| LilyPond | ly | ob-doc-lilypond | |
| Lisp | lisp | ob-doc-lisp | |
| Lua | lua | ob-doc-lua | |
| MATLAB® | matlab | ob-doc-octave-matlab | |
| Maxima | max | ob-doc-maxima | |
| Node.js | js | ob-doc-js | |
| OCaml | ocaml | ||
| Octave | octave | ob-doc-octave | |
| PlantUML | plantuml | ob-doc-plantuml | |
| Python | python | ob-doc-python | Jack Kamm |
| R | R | ob-doc-R | Jeremie Juste |
| Ruby | ruby | ||
| SQLite | sqlite | ob-doc-sqlite | Nick Savage |
Encore une fois, nous venons juste d’effleurer les possibilités d’org-babel.
Personnalisation #
Tu remarqueras que si tu exportes le document C-c C-e l o, le résultat n’est pas
mal, mais il y a des imperfections…
Par exemple, l’affichage du nombre \(ra\) avec ses 1 013 chiffres pose problème.
Plusieurs possibilités s’offrent à toi:
- Modifier le document LaTeX. C’est une solution facile, si tu maîtrises LaTeX, mais pas recommandée car après tu dois gérer deux documents qui vont être dé-synchroniser.
- Tordre un peu org-mode pour obtenir le résultat attendu. Cela nécessite de bien connaître LaTeX et babel …
ra
\numprint{31622776601683793319988935444327185337195551393252168268575048527925944386392382213442481083793002951873472841528400551485488560304538800146905195967001539033449216571792599406591501534741133394841240853169295770904715764610443692578790620378086099418283717115484063285529991185968245642033269616046913143361289497918902665295436126761787813500613881862785804636831349524780311437693346719738195131856784032312417954022183080458728446146002535775797028286440290244079778960345439891633492226526120677926516760310484366977937569261557205003698949094694218500073583488446438827311092891090423480542356534039072740197865437259396417260013069900009557844631096267906944183361301813028945417033158077316263863951937937046547652206320636865871978220493124260534541116093569798281324522970007988835237595853285792513629646865114976752171234595592380393756251253698551949553250999470388439903364661654706472349997961323434030218570521878366763457895107329828751579452157716521396263244383990184845609357626020316768042407}

